CrIS L1B Glint calculation

The sun glint calculation used in the initial versions of the CrIS L1B product uses a spherical earth approximation, meaning the glint location will be somewhere on the great circle arc connecting satellite nadir and the subsolar point. Glint occurs at the point on this arc where the solar zenith angle and sensor zenith angle are equal. So we can get a vector representing the sun glint location ($v_{glint}$) by starting with a vector for satellite nadir ($v_{sat}$) and rotating toward the solar vector ($v_{sun}$) by some angle $\phi$.

Before any rotation, at the nadir location, we have a satellite zenith angle of zero and some solar zenith angle $\theta_{sun}$.

The location on the surface resulting from rotating $v_{sat}$ toward $v_{sun}$ by $\phi$ will have a solar zenith angle reduced by the amount of the rotation, $\phi_{sun} = \theta_{sun} - \phi$.

The dependence of sensor zenith angle on $\phi$ is shown in a diagram below. The relationship given earth radius $r$ and satellite altitude $a$ is

$$\phi_{sat} = \arctan{\left(\frac{r \sin{\phi}}{r + a - r \cos{\phi}}\right)} + \phi$$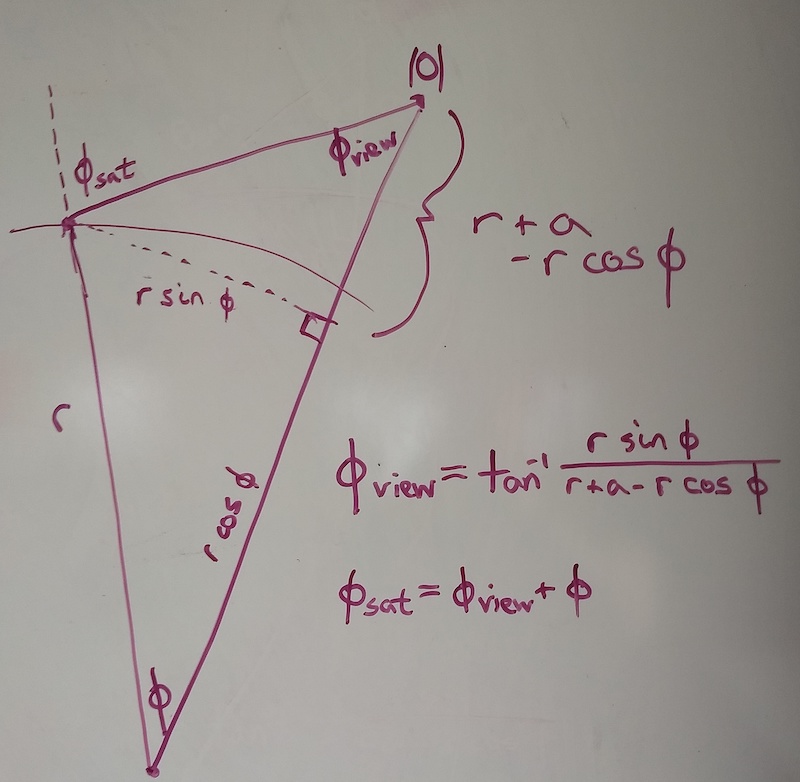

So the goal is to find $\phi$ such that $\phi_{sat} = \phi_{sun}$. Our current implementation does that using SciPy's brentq method to numerically find a zero to the function $\phi_{sat} - \phi_{sun}$ on the interval $[0, \theta_{sun}]$, like so:

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import root_scalar

earth_radius = 6371.
sat_height = 830.

theta_sun = np.radians(np.linspace(0., 180.))

def glint_equation(phi, theta_sun, r, a):
    return np.arctan((r * np.sin(phi)) / (r + a - r * np.cos(phi))) + (2 * phi) - theta_sun

phi = np.array([
    root_scalar(glint_equation, args=(x, earth_radius, sat_height), bracket=[0., x]).root
    for x in theta_sun])
plt.plot(np.degrees(theta_sun), np.degrees(phi))
plt.title('Glint displacement vs solar zenith at nadir')
plt.xlabel(r'$\theta_{sun}$ (deg)')
plt.ylabel(r'$\phi$ (deg)')
None

Performing the rotation can be done using a unit vector ($u_{sat}$) in the direction of $v_{sat}$ and a second unit vector ($u_{toward}$) in the direction of $v_{sat}$ rotated 90 degrees toward the solar vector, which can be obtained by normalizing $(v_{sat} \times v_{sun}) \times v_{sat}$. Then we can find the glint vector via:

$$v_{glint} = |v_{sat}|(u_{sat} \cos{\phi} + u_{toward} \sin{\phi})$$