The VisAD Tutorial

Section 4 -  Three-dimensional displays

[Section 3] [Home] [Section 5]

In this section we will use 3-D displays only, but we'll not restrict our discussion to functions involving only three RealTypes. We shall also introduce a few other VisAD widgets.

4.1 Three-dimensional display

We shall use the example program P3_09, make very little changes to it, in order to have the MathType displayed in 3-D.
Remember, the MathType reads: 
( (latitude, longitude) -> (altitude, temperature) )
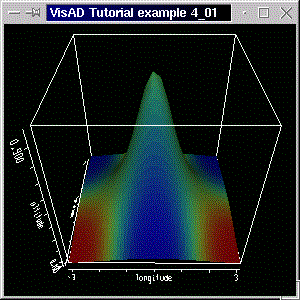
We want to display altitude in the z-axis and color the surface according to the temperature. To to that, first we need a display which has a z-axis: 
display = new DisplayImplJ3D("display1");
But note the different import statement: 
 import visad.java3d.DisplayImplJ3D;
The difference to the 2-D displays used so far isn't, well, only the "3", indicating it's a 3-D display. In fact, you might try changing the 2-D to a 3-D display in the previous example programs to see the difference. The lines and planes of the examples seen so far would simply be drawn at z=0. Three-dimensional displays have a third spatial dimension, and therefore allow for other DisplayRealTypes, that is, allow for different data depictions. To map altitude to z-axis we create the ScalarMaps 
altZMap = new ScalarMap( altitude,  Display.ZAxis );
and we color the surface according to the temperature: 
tempRGBMap = new ScalarMap( temperature,  Display.RGB );
We add these maps to the display and do the rest as usual.
You can see the complete code here.

Running the program will generate a window with a 3-D display like below:

A 3D display allows more DisplayRealTypes than a 2D display does and has other behavior, too. By dragging the left mouse button on the display you can rotate the cube. Dragging with the left mouse button and with the shift key pressed zooms the scene in and out. Dragging with the control key pressed tranlates the scene. Pressing and dragging the middle mouse button (on two-button mouse emulated by simultaneously clicking both buttons) shows a 3-D cross cursor that moves with the mouse. The values of the RealTypes at the cursor's position are shown on the upper left corner of the display.

You have seen how easy it is to jump from 2-dimensional to 3-dimensional data depiction. You might try experimenting with other DisplayRealTypes. The code for this example already includes the ScalarMaps 

altRGBMap = new ScalarMap( altitude,  Display.RGB );

tempZMap = new ScalarMap( temperature,  Display.ZAxis );
Of course, you need to add them to the display, and have the other ScalarMaps not added. (By the way, you can clear the maps associated with a display by calling the display method clearMaps(). But first you need to remove the references, which can be done with the display methods removeAllReferences() or removeReference( ThingReference ref ).) Implementig the changes, compiling and running the example will generate a screenshot like below.

Note the cursor showing the coordinates with units. You can, off course, color the surface according to RealType that is mapped to the z-axis. Just use two ScalarMaps, with DisplayRealTypes ZAxis and RGB and the same RealType (temperature or altitude). Try doing these changes, it's worth it!

[Top] [Home] [Back]

4.2 Using a ContourWidget

If you recall, in section 3.6 we used a ContourControl to control some properties of the isolines. Although this is enough when you know how the isocontours are going to look like and that they are not going to change, you have the choice of using a ContourWidget to interactively change the isocontour properties during runtime. We shall use a different version of program example 4_01 to demonstrate the use of a ContourControl.
In section 3.9 we had a display with isolines, which were not colored according to their value, but according to another RealType. Although this might be a rare thing to do, it's so trivial to do in VisAD that you might like to do it often. In this example we change the previous program, so that altitude is mapped to ZAxis and to RGB, and temperature is mapped to IsoContour. This is nothing new. The new feature in this example is, a said, the ContourWidget, declared as: 
ContourWidget contourWid;
(don't forget that we have added the import statement: import visad.util.*; ) and created with 
contourWid = new ContourWidget( tempIsoMap  );
where tempIsoMap is temperature's IsoContour map. (You can only create a ContourWidget with an IsoContour map.) See the complete code here.

Running the program will generate a window like the screen shot below:

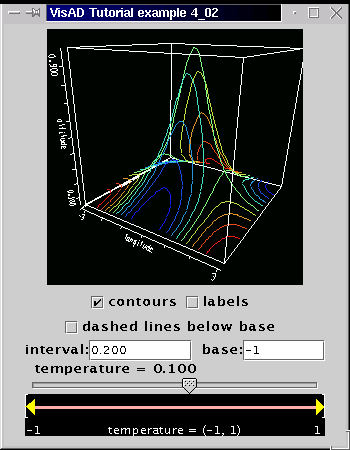
The ContourWidget allows for interaction regarding the isocontours. Not all switches are valid. Some of them only make sense with different types of data, as we shall see in section 4.12. Nevertheless, the ContourWidget is another nice tool in the visad.util package.

It should be clear by now how the ScalarMaps combined with the "right" DisplayRealTypes (that is, XAxis, YAxis, ZAxis, RGB, IsoContour, Red, Value, etc.) can give you the depiction you want.

In the next example we move on to another important topic: color control

[Top] [Home] [Back]

4.3 Using a LabeledColorWidget

In this section we introduce the LabeledColorWidget. Although VisAD provides ColorControl, we prefer to introduce the widget before the control, because we have already often used the DisplayRealType RGB without actually directly seeing how the standard VisAD color table looks like. The LabeledColorWidget also allows us to see and interactively manipulate the color table.
As we have seen in the previous two sections, there isn't a big conceptual leap between using a 2-D and a 3-D display. The logic behind ScalarMaps and DisplayRealTypes still apply; some DisplayRealTypes are not valid in 2-D displays, though. For example the DisplayRealType Display.ZAxis can only be used in 3-D displays.

Our example is a simplified version of the program of the previous section. We have the following MathType: 

( (latitude, longitude) -> altitude )
altitude is mapped both to ZAxis and to RGB. We have included the altitude values in the code. There are 6 (rows) times 12 (columns) altitude values in an array double[6][12]. Our domain set is the set 
domain_set = new Linear2DSet(domain_tuple, 6000.0,     0.0, NROWS,
    					      0.0,  10000.0, NCOLS);
where NROWS and NCOLS are the number of rows and columns, respectively. Note too the boundary values of the Set, indicating that latitude starts at 6000.0 and ends at 0.0, while longitude starts at 0.0 and ends at 10000.0. The actual altitude values are given by 
double[][] alt_samples = new double[][]{
  {3000.0,   3000.0,   6500.0,   4000.0,   3500.0,   4000.0,   5500.0,   4000.0,   4000.0,   4000.0,   5000.0,   1000 },
  {1000.0,   1500.0,   4000.0,   3500.0,   6300.0,   4500.0,   4000.0,   3800.0,   3800.0,   3800.0,   5000.0,   6400 },
  {  0.0,      0.0,       0.0,   1500.0,   3000.0,   6500.0,   4500.0,   5000.0,   4000.0,   3800.0,   3800.0,   6200 },
  {-3000.0,   -2000.0,   -1000.0,    0.0,   1500.0,   1000.0,   4000.0,   5800.0,   4000.0,   4000.0,   3900.0,   3900 },
  {-3000.0,   -4000.0,   -2000.0,   -1000.0,  0.0,   1000.0,   1500.0,   4000.0,   5700.0,   4500.0,   4000.0,   4000.0 },
  {-6500.0,   -6000.0,   -4000.0,   -3000.0,   0.0,   100.0,   1500.0,   4500.0,   6000.0,   4000.0,   4000.0,   4000.0 }};
Note that the minimum altitude value (-6500.0) is at the bottom left "corner" of the array. The Set boundaries mentioned above were chosen to match the "shape" of the array. (See figure below, where the minimum value is in fact at the bottom left corner of the display.)

This time we loop over rows and columns in a different way. We still have a 'flat' array: double[][] flat_samples = new double[1][NCOLS * NROWS]. The actual altitude values are put into this with two for-loops (as in the examples of section 3), but using an index variable, which "counts" the position of the samples in the flat array: 

int index = 0;

for(int c = 0; c < NCOLS; c++)
  for(int r = 0; r < NROWS; r++){

    // set altitude
    flat_samples[0][ index ] = alt_samples[r][c];

    // increment index
    index++;
  }
These for-loops do exactly the same as those of section 3. The only advantage of doing this is that the variable index counts the position of the samples, so it's easier for the user to understand what's happening.

The interesting feature of this example, though, is the use of a LabeledColorWidget. This widget allows users to visualize how a RealType is mapped to a color table. Some direct manipulation of the color table is also possible.
To create such a cute widget simply do: 

labelCW = new LabeledColorWidget( altRGBMap );
where altRGBMap is altitude's RGB ScalarMap. We then add the widget to the Java frame.

The code for this example is available here. Running the program with "java tutorial.s4.P4_03" generates a window like the screen shot below.

On the left we have the 3-D display, with altitude plotted against longitude and latitude. (Note that axes were auto-scaled.)

As already mentioned, the LabeledColorWidget allows interaction, too. The arrow just below the rainbow-colored bar can be moved by dragging with the left mouse button. The value of the RealType which is mapped to RGB and which is attached to the LabeledColorWidget is shown according to the arrow's position (note the that the altitude values vary from -6500 to 6500).
Above the bar you can see the distribution curves of the red, green and blue components. Click the left mouse button on a top part of the widget and drag to change either the red, green or blue distribution curves. The colored bar changes accordingly and so does the display. To switch between the color components click with either the middle or the right mouse button.
With the Reset button you can reset the color table and with the Gray Scale button you create a gray scale color table (that is, red, green and blue components increase linearly from 0.0 to 1.0).

Surely the LabeledColorWidget is a stunning widget, but there are times when you want to define your own color table. In the next example we'll show you how to do that.

[Top] [Home] [Back]

4.4 Defining a color table

In this section we will use a color table with length 8. Color tables in VisAD are defined in arrays like float[3][length]. The 3 components are red, green and blue components. Our color table is simply created as follows: 
    myColorTable = new float[][]{{0.0f, 1.0f, 0.0f, 0.0f, 0.0f, 1.0f, 1.0f, 1.0f},  // red component
     			         {0.0f, 0.0f, 1.0f, 0.0f, 1.0f, 0.0f, 1.0f, 1.0f},  // green component
     			         {0.0f, 0.0f, 0.0f, 1.0f, 1.0f, 1.0f, 0.0f, 1.0f}}; // blue component

As said, the values in the table are interpreted as red, green and blue components. (Remember, values range from 0 to 1.) The first color in the table is black: (r,g,b) = (0,0,0). The second color is red: (r,g,b) = (1,0,0). The following colors are green, blue, cyan, magenta, yellow and white.

The actual difference to the previous example is in the constructor of the LabeledColorWidget: 

labelCW = new LabeledColorWidget( altRGBMap, myColorTable );
The widget is created with our table as the initial color table.

Please not too that we have set the ranes of the latitude and of the altitude map with the calls: 

latMap.setRange(-2000.0f, 8000.0f);
altMap.setRange(-10000.0f, 10000.0f);

The code for this example is available here. Running the program with "java tutorial.s4.P4_04" generates a window like the screen shot below.

You can see the same surface and widget of the previous example. The colors, however, are those given by the color table. You can, off course, manipulate them with the help of the widget.

[Top] [Home] [Back]

4.5 More Color Control: Using ColorControl and Texture Mapping

As already mentioned, ColorControl provides methods for controlling the color, without the need of a LabeledColorWidget.

We use the same table of the previous example, but no LabeledColorWidget. To set the color table we first get hold of the ColorControl, from the RGB map: 

colCont = (ColorControl) altRGBMap.getControl();
and finally set the color table: 
colCont.setTable( myColorTable );
That was it! We changed the color without a widget.

So that this example doesn't become boring, we make a call of a GraphicsModeControl's method. Remember from section 2.1 that we create a GraphicsModeControl with: 

GraphicsModeControl dispGMC = (GraphicsModeControl)  display.getGraphicsModeControl();
With the following call we disable texture mapping: 
dispGMC.setTextureEnable(false);

By disabling texture mapping we make the polygons have interpolated colors instead of textures. This removes the tesselated texture, like it was seen in the previous examples, and causes the smoother appearance.

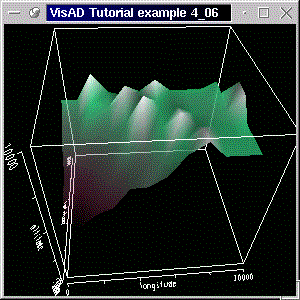
The code for this example is available here. Running the program with "java tutorial.s4.P4_05" generates a window like the screen shot below.

The color table is the same as the one used in the previous example, but it has been implemented with the setTable( float[][] ) method of ColorControl. The visual difference is due to use of texture.

[Top] [Home] [Back]

4.6 Transparency: Using an Alpha Map

In this example we'll create a ScalarMap whose DisplayRealType is Display.Alpha. Alpha determines how transparent an object is. In a ScalarMap, the degree of transparency will be determined by the RealType. We'll use the previous program to demonstrate this.

We simply decide that the higher our surface is, the more opaque (less transparent) it will be. This means, the higher the value of the RealType altitude, the less we can see through the surface at that point. This is achieved by creating a ScalarMap like 

altAlphaMap = new ScalarMap( altitude,  Display.Alpha );
and by adding it to the display, as usual.

In this section we also take the opportunity to show how you would create a color table using a loop. Our new colour table is given by an array float[3][ tableLength ]. We set the red (first) component of the table to decrease linearly (from 1 to 0) with the table length, the green (second) component to increase linearly (0 to 1), and set the blue (third) component to have a constant value of 0.5 (that is, 50% of maximum blue). Remeber, component values vary between 0 and 1. The code to create the table is as follows: 

int tableLength = 10;

myColorTable = new float[3][tableLength];

for(int i=0;i < tableLength;i++){

  myColorTable[0][i]= (float) 1.0f - (float)i / ((float)tableLength-1.0f); // red component
  myColorTable[1][i]= (float) (float)i / ((float)tableLength-1.0f); // green component
  myColorTable[2][i]= (float) 0.50f; // blue component

}
We force, however, the top of the color table to be white: 
myColorTable[0][9]=1.0f;
myColorTable[1][9]=1.0f;
myColorTable[2][9]=1.0f;

We implement the color change like we did in the previous section: 

colCont = (ColorControl) altRGBMap.getControl();

colCont.setTable( myColorTable );

You can see the result of the use of a transparency map in the screenshot below and have a look at the code here.

In practice you might use alpha for modelling transparent clouds, or for making some soil layers transparent, so that you can see the other layers under them. In the next example we'll do that. We shall create another surface, based on the given data, and set the top layer with constant transparency, by using ConstantMaps.

Before we carry on, you might want to know that the LabeledColorWidget can be created with an RGBA (red, green, blue and alpha) map. The color-alpha table is then an array like float[4][length] and direct manipulation of the RGBA-table is possible.

[Top] [Home] [Back]

4.7 More Transparency: Using a ConstantMap with Alpha Value

If you remember, back in section 2.4 we used an array of ConstantMaps to set the color of the points to constant red. We shall now use an an array of ConstantMaps to set the Alpha value of the surface to a constant transparency. There is no mistery in doing this, but we'll take the opportunity to introduce a method from the FlatField class: derivative(). This method computes the derivative of a function (that is, of a FunctionType contained in the FlatField) with respect to some quantity (that is, a RealType). The derivative() method returns a FlatField, which is the basis of a new surface.

Before we create the transparency ConstantMaps, we generate the other surface. We simply decide that we want a surface of the slope of the first surface in the x-direction (longitude). To put it mathematically correct, we want the first derivative of altitude with respect to longitude. if you're not quite sure how to calculate that, don't worry, VisAD will take care of that for you.

Recall that we have the FunctionType 

( (latitude, longitude) -> altitude )

In mathematical notation that reads altitude = f(latitude, longitude) (in words: altitude is a function of latitude and longitude), and we shall calculate slope = derivative of altitude with respect to longitude (we are assuming, for the sake of simplicity, that slope is measured in one direction olny).

We will need:

  1. A Data object to hold slope data; this will be represented by a FlatField;
  2. A new RealType: slope; (Remember, slope has a unit of its own, but are not going to define the unit, because we are going to get it for free from the FlatField.)
  3. A ScalarMap for slope, as we want to color the slope surface; and finally we'll need
  4. A DataReference to link the data to the display. (Please bear in mind that slope is a function of altitude, and therefore also a function of latitude and longitude.

4.7.1 Creating the new surface's data

We start off by declaring the FlatField: 

FlatField slope_vals_ff ;

To calculate the derivative we do hardly any work: 

slope_vals_ff = (FlatField) vals_ff.derivative( longitude, Data.NO_ERRORS );
The line above means: calculate the derivative of altitude with respect to longitude, and assume no errors (that is, error mode is Data.NO_ERRORS; VisAD includes error propagation, which is calculated according to the chosen mode). Remember that in VisAD a FlatField represents a mathematical function, and thus is only natural that a FlatField would offer a mathematical operation such as differentiation. Note that the method returns a FlatField.

If you are a bit lost, don't worry. You must bear in mind that, when we constructed the FlatField vals_ff for the altitude values with 

vals_ff = new FlatField( func_domain_alt, domain_set);
we said how the function looks like: func_domain_alt is a function of domain (latitude, longitude) to altitude, and domain_set is the set which "says" how the data looks like. All the information is encapsulated in the FlatField. To make it a bit clearer, we get the function slope = f(latitude, longitude): 
FunctionType func_domain_slope = (FunctionType) slope_vals_ff.getType();

4.7.2 Getting the RealType slope

So, slope is a function of latitude and longitude just as altitude is. As you know, in VisAD we call a RealType like slope or altitude the range of a FunctionType. So we make the call 
RealType slope = (RealType) func_domain_slope.getRange();
to get the range of this newly generated function (that is, the variable or variables which are a function of some other variables, also known in the mathematical jargon as "dependent variables"). The range is always a MathType (remember, the super class of RealType, RealTupleType, etc). For example, the range of the function ( (latitude, longitude) -> (altitude, temperature) ) is RealTupleType formed by altitude and temperature. In our case the range is simply slope, which is thus a RealType.

4.7.3 Creating an RGB ScalarMap for slope

Using the brand new RealType we create an RGB map: 
ScalarMap slopeRGBMap = new ScalarMap( slope,  Display.RGB );
Again, no mistery in the previous line. We are almost done, except by the DataReference.

4.7.4 Creating a DataReference for slope's data

We can't forget to create the DataReference and to set its data: 
DataReferenceImpl data_ref2 = new DataReferenceImpl("data_ref2");
data_ref2.setData( slope_vals_ff );
So we're finished with creating the new surface. We have now to decide how we want to draw it. In the beginning of this section we said we were going to use ConstantMaps to set the altitude's surface to a constant alpha value. We do this by creating such a map (actually, an array of ConstantMaps): 
ConstantMap[] constAlpha_CMap = { new ConstantMap( 0.50f, Display.Alpha) };
with 50% alpha value, and by adding the DataReference with the ConstantMap to the display: 
display.addReference( data_ref, constAlpha_CMap );
We choose to draw the slope's surface at a constant z value, that is at z = -1. This is done with the ConstantMap array: 
ConstantMap[] constZ_CMap = { new ConstantMap( -1.0f, Display.ZAxis)};
The DataReference is added to the display as 
display.addReference( data_ref2, constZ_CMap );
In the code, though, this is done in the inverse order. We first add the slope's reference and then the surface's reference.

The result can be seen in the following screenshot. The code for the application is, as usual, available here.

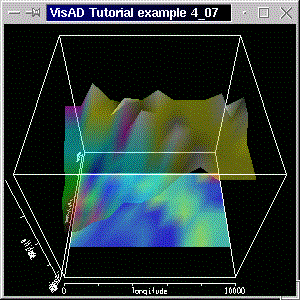
You can see the original surface, with the same colors as before, but with a constant transparency given by the constant alpha value map. The slope surface is drawn at a constant z = -1 value. (The cube has its center at (x,y,z) = (0,0,0) and side length equal to 2.)

It wasn't a straight forward matter to calculate the derivative. You might need to read this section again and also work through the code, till you can grasp what's been done. Nevertheless, you've met a very powerful method. Hopefully you'll realize how those Datamethods, used in conjunction with VisAD's MathTypes can simplify your work. Also try changing the values of the ConstantMaps and/or including a ConstantMap like ConstantMap( 3.50f, Display.PointSize ), like we did in section 2.4.

You could also add a ConstantMap alpha map to the whole display with 

display.addMap( new ConstantMap( 0.50,  Display.Alpha ));
thus setting a constant transparency to all objects in the display.

Don't forget that you can add any number of references (data objects) to a display. In this section we added just another one, but we chose to introduce a method from FlatField class. This class includes other powerful methods like evaluate() and resample(), which can be used for evaluating the value of a function at a given value of the dependent variables and for interpolation, respectively.

In the next section we move on to consider 3-D sets in 3-D displays.

[Top] [Home] [Back]

4.8 Volume Rendering: Using an Integer3DSet

The Integer3DSet is the 3-D analogous to the Integer1DSet and to the Integer2DSet. The domain of such a set is 3-dimensional, and the set samples are integer values. Three-dimensional sets are the basis of volume rendering. In this example we use an Integer3DSet to render a volume.

We start off by defining some RealTypes 

red = new RealType("RED", null, null);
green = new RealType("GREEN", null, null);
blue = new RealType("BLUE", null, null);
and the domain: 
domain_tuple = new RealTupleType(red, green, blue);
The RealTypes are arbitrary and will be plotted in the x, y and z-axis.

The dependent variable is the RealType 

rgbVal = new RealType("RGB_VALUE", null, null);

The RealTypes red, green and blue could be the dimensions of a space (like length, width and height) and the RealType rgbVal could be some quantity in this space, temperature, for example.

The function is defined as usual 

func_domain_rgbVal = new FunctionType( domain_tuple, rgbVal);
and the number of samples in our "cube" as given by 
int NCOLS = 32;
int NROWS = 32;
int NLEVS = 32;
We then construct the set, with the number of samples above 
domain_set = new Integer3DSet(domain_tuple, NROWS, NCOLS, NLEVS );
Note that we make no distiction between "number of samples" and "size of the cube", as we're dealing with an integer set. This is not the case for a linear set, where not only do you define the number of samples, but also the dimensions: starting at some value, and ending at some other value, with an arbitrary number of samples, as we shall see soon.

The next step concerns the actual values of rgbVal. We decide tht the higher the index of the sample, the higher the value

Those values fit in a "flat" array: 

double[][] flat_samples = new double[1][NCOLS * NROWS * NLEVS];
and they are set with the next following for-loops 
  int index = 0;

  for(int l = 0; l < NLEVS; l++)

    for(int c = 0; c < NCOLS; c++)

      for(int r = 0; r < NROWS; r++){

	    // set rgbVal values
	    flat_samples[0][ index ] =   index;

	    // increment index
	    index++;
    }

We've done this before, but in two dimensions. We then create the FlatField and feed it with the samples generated above: 

vals_ff = new FlatField( func_domain_rgbVal, domain_set);

vals_ff.setSamples( flat_samples , false );

Rendering is given by the following choice of ScalarMaps: 

redXMap = new ScalarMap( red,    Display.XAxis );
greenYMap = new ScalarMap( green, Display.YAxis );
blueZMap = new ScalarMap( blue, Display.ZAxis );

rgbMap = new ScalarMap( rgbVal,  Display.RGB );
Nothing new here either: domain types mapped to cube dimensions and color mapped to our independent variable. We add the maps to a 3-D display and do the other stuff as usual: set the Data Reference with the FlatField and add the reference to the display.

The result can be seen in the following screenshot. The code for the application is available here.

The volume is colored according to the index. At the bottom of the cube, where index is low, we have blue (recal that the standard color table varies from blue, through green, to red), and at the top we have higher index values, and thus red.

In the next example we vary the choice of ScalarMaps and see what happens to the cube.

[Top] [Home] [Back]

4.9 RGB Color Cubes

This example is a simple variation of the previous. We forget about the value of rgbVal (that is, we don't add the rgbMap to the display. Instead, we create and add the maps: 
redMap = new ScalarMap( red,  Display.Red );
greenMap = new ScalarMap( green,  Display.Green );
blueMap = new ScalarMap( blue,  Display.Blue );
We have also choosen less samples (8 for each side).
The result can be seen in the following screenshot. The code for the application is available here.

You can now see the individual points (or voxels) of the Integer3DSet. We have made them bigger with the GraphicsModeControl's call: 

dispGMC.setPointSize(40.0f);

Note that the color values are given by the respective values of the cube sides. From the distance, the displays shows a cube like the rgb-color-cube. If you zoom in (press shift key and left mouse button and move the mouse), you can see the individual voxels.

[Top] [Home] [Back]

4.10 More Volume Rendering: Using a Linear3DSet

As you probably already know, the Linear3DSet different from the Integer3DSet in that it uses non-integer as samples. We have already used 1-D and 2-D linear sets before. Three-dimensional linear sets are 3-D analogous of those other sets. In this section we use example 4.9. We employ, however, a Linear3DSet, but feed the FlatField with different data, but only to get a different color distribution. We also take the opportunity to use a different projection policy (instead of the perspective projection we've used so far).

We still use the same RealTypes, domain, and FunctionType of example 4.8. The only difference is the different domain set: 

domain_set = new Linear3DSet(domain_tuple,
                              -Math.PI, Math.PI, NROWS,
                              -Math.PI, Math.PI, NCOLS,
                              -Math.PI, 0,       NLEVS );

Note the use of upper and lower boundaries for all three dimensions.For the first two dimensions we have 32 samples for each dimension (given by NROWS and NCOLS). We have however only 16 samples for the number of levels (NLEVS), that is, for the RealType blue. We complement that with a call: 

blueZMap.setRange(-Math.PI, Math.PI );

If we hadn't done that, than the range of the blueZMap map would still have matched those given by the set, but would've been autoscaled to fill the whole display box. Calling the method above keeps the right dimensions.

Also note that we got the set samples with the call 

float[][] set_samples = domain_set.getSamples( true );
They were used to make some values up for the independent variable.

As promised, we change the projection policy with the GraphicsModeControl: 

dispGMC.setProjectionPolicy(DisplayImplJ3D.PARALLEL_PROJECTION);

The other valid projection policy is DisplayImplJ3D.PERSPECTIVE_PROJECTION, which is standard and thus has been used so far.

You can have a look at the code which generates a figure like the screenshot below.

As said, the difference between a linear and an integer set is that the latter is an specialization the the former, in that its samples are a progression of integers. (But all other methods used for the display in this section apply equally for the integer set.)

[Top] [Home] [Back]

4.11 Volume Rendering with RGBA Map

In section 4.6 we mentioned that you can use a LabeledColorWidget with an RGBA map, rather than with an RGB map. The only difference is that the "color" table associated with the RGBA map has 4 components. The LabeledColorWidget behaves just like in the "pure color" version, allowing you to manipulate all 3 color components plus the alpha component. In this section, we adapt the previous example to use a LabeledColorWidget with an RGBA map. We shall also create our own "color-alpha" table and initialize the widget with it. The final modification is the use of a SelectRangeWidget, linked with one of the RealTypes of the domain. In a sense, this section brings nothing new. It's jut a combination of other things we've seen so far.

Let's start with the color-alpha table. Remember, such a table looks like float[ 4 ][ tableLength ], that is red, green, blue and alpha components in the first dimension, and a number tableLength of values. We create the table with: 

int tableLength = 15;

myColorTable = new float[4][tableLength];

for(int i=0;i < tableLength;i++){

  myColorTable[0][i]= (float) i / ((float)tableLength-1.0f); // red component
  myColorTable[2][i]= (float) 1.0f - (float)i / ((float)tableLength-1.0f); // blue component

  if(i<(tableLength)/2){ // lower half of table

    myColorTable[1][i]= 2.0f *(float) i / (tableLength-1); // green component
    myColorTable[3][i]= 0.8f * myColorTable[0][i];

  }
  else{ // upper half of table

    myColorTable[1][i]=  2.0f - 2.0f *(float)i / ((float)tableLength-1); // green component
    myColorTable[3][i]= 0.8f * myColorTable[2][i];// alpha component

  }
}
That is, the table is 15 units long. Inside the for-loop with set the individual components. The red component increases linearly (from 0 to 1) with the table units, whereas the blue component decreases linearly (from 1 to 0). After that we decide to make the green component increase linearly, but twice as fast as the red component. The alpha component has 80% of the value of the red component. But those green and alpha values are only for the lower half of the table. For the upper half we make green decrease from 1 to 0, and make the alpha to be 80% of the blue value. Confusing? Wait till you see the result in the LabeledColorWidget.

No, we're not happy yet (but not because it's not confusing enough). We decide to give the aplha component a special look by doing: 

// make lower edge "sharp"; alpha values only
myColorTable[3][0]= (float) 1.0f; // alpha component
myColorTable[3][1]= (float) 1.0f; // alpha component

// make upper edge semi-transparent; alpha values only
myColorTable[3][13]= (float) 0.5f; // alpha component
myColorTable[3][14]= (float) 0.5f; // alpha component
The first two lines of code above make the first two values of the alpha component opaque. That is, the RealType linked to this RGBA map (and thus linked to the table) will have its lower values blue and opaque. The last two lines of code will make the data with highest values of the RealType red and "half-transparent".

Let us not forget the LabeledColorWidget: 

labelCW = new LabeledColorWidget( rgbaMap, myColorTable );
Where rgbaMap is simply: 
rgbaMap= new ScalarMap( rgbVal,  Display.RGBA );
(Remember, rgbVal is our RealType mapped to Display.RGBA by the means of the ScalarMap above. Also, don't forget to add this map to the display, before you reate the widget.)

We have also promised a SelectRangeWidget. For that we need a ScalarMap with Display.SelectRange: 

greenRangeMap = new ScalarMap( green, Display.SelectRange );
Yes, you guessed it right. The chosen RealType is green. (To clear things up a bit: our data is contained in a parallelepiped. The domain of this space is domain_tuple = new RealTupleType(red, green, blue). The RealType rgbVal is the dependent variable.)

After adding the above map to the display, we create the SelectRangeWidget: 

selRangeWid = new SelectRangeWidget( greenRangeMap );

and we're finished!

The complete code is available. Below is a screenshot of the program.

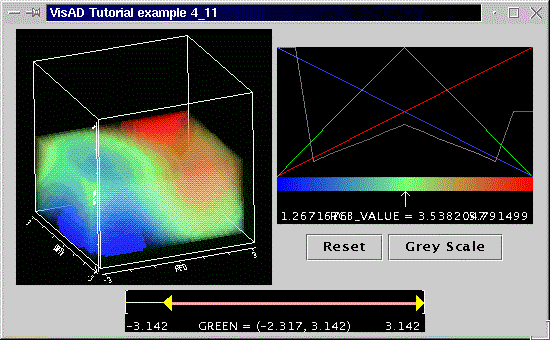
The first thing to notice on the picture above is that our former solid parallelepiped is now transparent (compare with the previous example). The degree of transparency is, however, not constant. It varies according to the alpha component of the color-alpha table (see the gray line of the LabeledColorWidget). As said, the LabeledColorWidget behaves as described in section 4.3, but now you can manipulate all 4 components of the table.

The SelectRangeWidget allows you to select the range in which the RealType green (the width of the parallelepiped) will be drawn. You should take your time to experiment with both widgets. Try, for example, changing the components of the color table by clicking and dragging on the LabeledColorWidget. You could also try adding another couple of SelectRangeWidgets for the other dimensions of the parallelepiped.

[Top] [Home] [Back]

4.12 Projection Matrix and Aspect Ratio

We saw in section 4.10 how we can change the projection policy. We were, however, limited to two types of projection policy. Every display, be it 2-D or 3-D, has a matrix controlling the projection. The actual control of this matrix is provided by the ProjectionControl. In this example we change the aspect ratio of the display and then print new projection matrix.

We use the previous example and make no changes to its data structure. The only change we make regards the boundaries of the set, which are now 

domain_set = new Linear3DSet(domain_tuple,
                            -Math.PI, 2.0*Math.PI, NROWS,
                            -Math.PI, Math.PI, NCOLS,
                            -Math.PI, 0.0,     NLEVS );
We do that so that the ranges are in the ratio 3 to 2 to 1.

First we get the ProjectionControl: 

ProjectionControl projCont = display.getProjectionControl();
To change the aspect ratio we define an array with the ratios 
double[] aspect = new double[]{1,0.66,0.33};
(note that the values are in the ratio 3:2:1) and do 
projCont.setAspect( aspect );
We get the projection matrix with 
double[] projMatrix = projCont.getMatrix();
Running the code, the 16 values of the matrix get printed out in the command window. There's also a matrix in the code, which can be used to set a new projection. Just uncomment the necessary line.

The complete code is available. Below is a screenshot of the program.

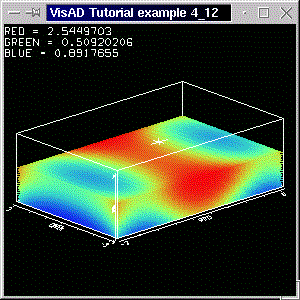
Note that the ProjectionControl can also be used for 2-D displays. In this case, the matrices are an array like double[1][6]. The 3-D case uses matrices with 16 elements, in an array double[1][16]. The aspect ratio of 2-D displays is given by arrays like double[1][2].

Changing the aspect ratio implies a change in the projection matrix. The matrix that is printed out in this example is the transformed matrix. A value greater than one in the aspect ratio array means a magnification. That's why we chose 1,0:0,66:0,33, rather than 3:2:1 (but you can try changing those values!). Finally note that by changing the aspect ratio, you change the shape of the cursor.

[Top] [Home] [Back]

4.13 Using the ContourWidget with Volume Data

In section 4.2 we introduced the ContourWidget. We saw there that not all of its controls were valid, and that they depended from the type of data. In this section we add a ContourWidget to the previous example and see how it changes data depiction.

We need a ScalarMap with IsoContour, off course: 

rgbIsoMap = new ScalarMap( rgbVal,  Display.IsoContour );
As you see, we'll draw the isocontours of the RealType rgbVal. As our set is 3-dimensional, we don't expect to see isolines, but isosurfaces. That is, surfaces which have the same rgbVal value. We'll control this value with the help of the ContourWidget.

Dont' forget to add the map to the display before we create the ContourWidget as follows: 

contWid = new ContourWidget(rgbIsoMap);

The complete code for this example is available here. Below is a screenshot of the application.

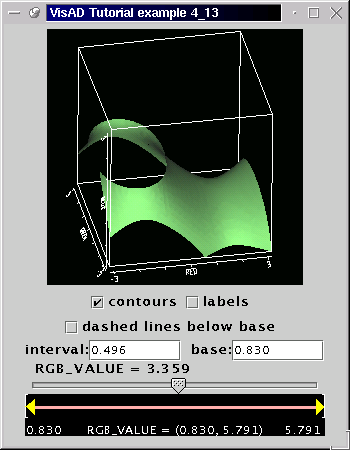
You can change the value of the isosurface by moving the slider. The data of this example is the same as that of the previous example (just some set boundaries were changed, and the aspect ratio change was removed). By adding the IsoContour ScalarMap, you can drastically change data depiction without changing the way your data is organized (as you probably know by know)

[Top] [Home] [Back]

4.14 More on Display Layout

In this section we take it easy and take the opportunity to introduce a few DisplayRenderer methods. The DisplayRenderer is the superclass for background and metadata rendering algorithms. There are a few of those in VisAD, and we'll come across some of them, later on in the tutorial. For now we are only interested in grabbing the DisplayRenderer of a display, and calling a few methods to change colors, turn off the display box and so on. It's also a good opportunity to change axes colors and names, while we are on the subject of display layout.

We take the last example and adapt it a bit to show some interesting methods. First we get the DisplayRenderer with 

DisplayRenderer dRenderer = display.getDisplayRenderer();
and the first useful thing we do with it is to set the background color: 
dRenderer.setBackgroundColor(Color.white);

Note that you can also change the foreground color, which will change both the axes, the box and the cursor colors. 

dRenderer.setForegroundColor(Color.gray);

With the DisplayRenderer we can also turn the box off: 

dRenderer.setBoxOn( false );

Although we haven't done it in the example (the code line is commented out), you might want to change the box color: 

dRenderer.setBoxColor(Color.gray);

The second change regards axes names. When a ScalarMap is created, it uses the name of the ScalarType as the axis label (in case is a map to one of the axes). This works fine, but has the disadvantage of not allowing some characters (as there are some constraints on a ScalarType's name). Furthermore, you might want to write a little more on the axis as only the name of the ScalarType. To set the axis label you call the ScalarMap method: 

redXMap.setScalarName("The RED Component");
where redXMap is a ScalarMap.

To change the color of an axis, you can do 

float[] r = colorToFloats(Color.red);
redXMap.setScaleColor( r );
Note that r is a float with RGB components between 0 and 1. The method colorToFloats(Color c) is just a convenience method to decompose a java.awt.Color into its RGB components. It returns a float array like float[]{ red, green, blue}, with values between 0 and 1. The method is included in the code for this example.

Although

You can see the results in the following picture. The complete code for this example is available here.

Note that each axis has its own color, and also has a customized label. The background color is somewhat dull, but you can choose your own color. Finally, the box is nowhere in sight, but now you know how to turn it on and off and know how to change its color.

In the next section we consider animation with VisAD.

[Top] [Home] [Back]

[Section 3] [Home] [Section 5]